Los métodos de transformación en HEC-HMS permiten generar el hidrograma de escorrentía superficial a la salida de una subcuenca a partir de la precipitación excedente calculada (precipitación que no se infiltra ni se almacena).

En esta ocasión, nos enfocaremos exclusivamente en los métodos de transformación disponibles en HEC-HMS, detallando su base conceptual, parámetros requeridos, aplicaciones recomendadas, ventajas y limitaciones. Se incluye además una tabla comparativa final que facilita la elección del método más apropiado según la escala del modelo, tipo de cuenca y objetivos del estudio.

Los métodos de transformación toman la precipitación excedente calculada en cada intervalo de tiempo y producen un hidrograma de escorrentía a la salida de la subcuenca. HEC-HMS ofrece ocho métodos de transformación en la versión actual, los cuales se dividen en dos enfoques principales:

• Métodos basados en hidrograma unitario (Unit Hydrograph, UH): Son técnicas sintéticas que usan la teoría del hidrograma unitario: suponen que la respuesta de la cuenca a una “lámina unitaria” de lluvia excesiva es constante en el tiempo (lineal e invariante). Incluyen los hidrogramas unitarios Snyder, SCS, Clark, además de opciones para hidrogramas definidos por el usuario (UH o curva S especificada). Estos métodos son conceptualmente simples y requieren parámetros empíricos (tiempos de atraso, factores de pico, etc.).
• Métodos basados en modelos físicos de ruteo hidráulico: Incluyen la onda cinemática (ruteo en un plano o red de planos/canales) y la onda difusiva 2D. Estos resuelven aproximaciones de las ecuaciones de Saint-Venant para modelar el movimiento del agua en la cuenca, capturando efectos no lineales de encharcamiento, almacenamiento y propagación con mayor realismo físico. Requieren más datos geométricos y computación, pero pueden representar mejor las dinámicas de flujo para eventos extremos o en áreas urbanas complejas.

A continuación se detallan cada uno de los métodos de transformación disponibles y sus parámetros:

Hidrograma Unitario del SCS (SCS UH, método del SCS)

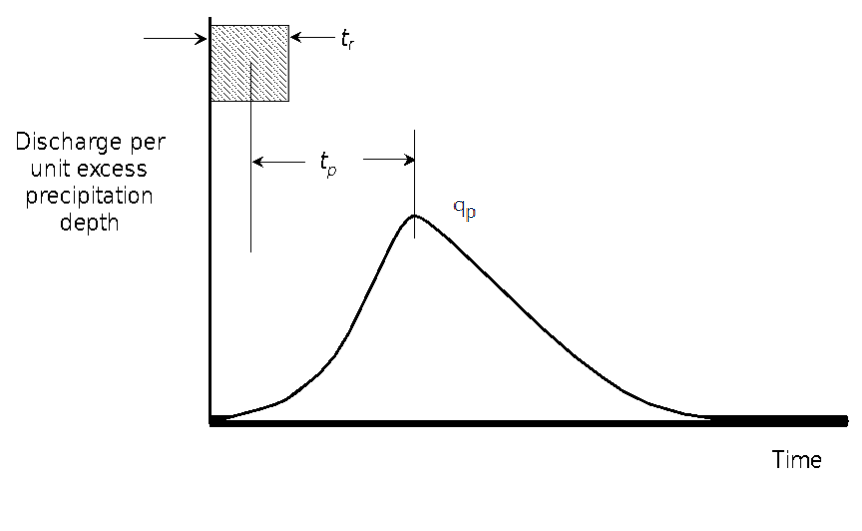
Es un hidrograma de forma fija, definido en términos porcentuales: el caudal q en cualquier instante es una fracción del caudal pico qp, y el tiempo es una fracción del tiempo al pico Tp (tiempo de ascenso). En el UH SCS estándar, aproximadamente el 37,5% del volumen ocurre antes del pico. La relación entre el lag (retardo) de la cuenca tp y la duración efectiva de la lluvia tr es: Tp = tr/2 + tp. El caudal pico viene dado por Qp = PRF . A/Tp , donde A es el área de la cuenca y PRF es el factor de pico. En el UH SCS estándar, PRF = 484 (sistema inglés), que corresponde a la forma adimensional clásica. Sin embargo, PRF puede ajustarse: terrenos empinados suelen tener PRF mayores (~600), y terrenos planos PRF menores (~100). Ajustar PRF cambia la agudeza del pico y la fracción de volumen antes del pico, adaptando el hidrograma a distintas pendientes o alargamientos de la cuenca.

Parámetros:

El método SCS en HEC-HMS requiere dos parámetros: el Peak Rate Factor (PRF) y el Lag time de la cuenca (tiempo de retardo, en minutos u horas). Por defecto, si no se indica lo contrario, se usa PRF = 484 (UH estándar).

El tiempo de retardo tp típicamente se relaciona con el tiempo de concentración Tc de la cuenca mediante tp (aproximadamente 0,6,Tc según recomendaciones del NRCS). En aplicaciones prácticas, Tc se estima sumando tiempos de recorrido en distintos tramos: escurrimiento laminar, escurrimiento somero, escurrimiento en cauce, usando fórmulas empíricas (como la fórmula de Kirpich para Tc o las de lámina/inmersión superficial del SCS). Con un Tc estimado, se calcula tp y así Tp para la lluvia de duración dada. En la implementación, el usuario suele ingresar directamente el lag time (tp), que se puede calibrar con hidrogramas observados o estimar como cierto porcentaje de Tc (50–75% de Tc según diversos estudios). El método SCS es apreciado por su simplicidad (solo requiere un tiempo de retardo) y se aplica frecuentemente tanto en cuencas rurales como urbanas pequeñas, ajustando Tc y/o PRF según el caso.

Su precisión esperada es razonable para cálculos preliminares y diseño, aunque al ser un UH genérico, puede no captar peculiaridades de cuencas muy planas o muy empinadas a menos que se ajuste PRF.

Hidrograma Unitario de Snyder

El método de Snyder (1938) es otro método sintético paramétrico, originalmente desarrollado para cuencas en las montañas Apalaches (EE.UU.) y luego aplicado ampliamente. Snyder definió un UH “estándar” mediante dos parámetros principales derivados de características geomorfológicas de la cuenca: el tiempo de retardo tp (tiempo entre el centro de masa de la lluvia excedente y el pico del hidrograma) y el caudal pico unitario qp (por unidad de área). Propuso fórmulas empíricas para calcular estos a partir de mediciones de la cuenca. En la implementación de HEC-HMS, el UH de Snyder se logra mediante una rutina de optimización que ajusta un UH tipo Clark equivalente a los parámetros Snyder especificados, por lo que internamente se aprovecha la flexibilidad del método de Clark pero conservando el estilo Snyder.

Parámetros

En HEC-HMS hay tres variantes: el método Snyder estándar, y dos calibraciones regionales especiales denominadas “Ft. Worth” y “Tulsa” (desarrolladas por distritos del USACE). Para el Snyder estándar, los parámetros requeridos son: el lag time tp (horas) y el coeficiente Cp (adimensional). Cp es el factor que influye en qp. Valores típicos reportados: Cp oscila 0,4–0,8 (0,5 nominalmente) y el coeficiente de tiempo Ct asociado al cálculo de tp suele ser 1,8–2,2 (varía 0,4 en montañosas a 8 en regiones costeras planas), aunque en HEC-HMS uno entra directamente tp y Cp. Para las variantes regionales:

• Ft. Worth (Texas): además de tp y Cp, requiere datos físicos de la cuenca para estimar esos parámetros: la longitud total del cauce L hasta el punto hidrológicamente más remoto, la longitud Lc hasta el centroide de la cuenca, la pendiente media del cauce principal (entre los puntos al 10% y 85% de L), el % de urbanización y el % de arena en suelos. Con regresiones, HEC-HMS calculará tp y Cp.
• Tulsa (Oklahoma): similar, pide L, Lc, pendiente 10-85%, y % de encauzamiento artificial (canalización), para usar fórmulas específicas de esa región.

En general, si no se usan esas opciones regionales, el usuario provee tp y Cp directamente (de calibración o literatura). El lag tp de Snyder a veces se estima con la fórmula: tp = Ct (Lc)^0.3 (si L en km, C constante de unidades), donde Ct es calibrado regionalmente.

Snyder es más complejo que SCS (más parámetros) pero puede adaptarse a diferentes tamaños de cuenca. Se recomienda para cuencas medianas donde no se cuenta con UH medido; original para cuencas rurales, aunque se han incorporado factores para urbanización.

Precisión esperada: con calibración regional puede proveer hidrogramas razonables, pero la incertidumbre de Ct y Cp es alta fuera de sus zonas de derivación. A menudo se prefiere calibrar directamente tp y Cp con eventos si hay datos. En HEC-HMS, tras computar un UH Snyder, se utiliza un equivalente de Clark para el ruteo real, por lo que no hay restricción de duración de lluvia (Snyder definía tr estándar de tp/5.5 pero el programa ajusta internamente si difiere). En resumen, Snyder requiere un poco más de esfuerzo en estimar parámetros, pero es útil para cuencas sin datos apoyándose en correlaciones geomorfológicas.

Hidrograma Unitario de Clark

El método de Clark (1945) es un enfoque de hidrograma unitario que explícitamente separa dos procesos: (1) la traducción (o propagación sin almacenamiento) del escurrimiento desde las distintas partes de la cuenca hasta la salida, y (2) la atenuación por almacenamiento en la cuenca.

A diferencia de SCS o Snyder, que tienen formas fijas, Clark construye un hidrograma unitario (UH) a partir de un histograma tiempo-área y un modelo de reservorio lineal. Conceptualmente, imagina que toda la cuenca recibe 1 unidad de lluvia instantánea (hidrograma unitario instantáneo); el histograma tiempo-área describe qué fracción del área contribuye flujo a la salida después de cierto tiempo (esencialmente, la distribución de tiempos de recorrido desde cada parte de la cuenca). Esto modela la traducción pura (sin pérdida) del caudal: inicialmente solo áreas cercanas aportan, luego áreas más lejanas van contribuyendo hasta el tiempo de concentración Tc cuando toda el área está drenando en la salida.

Después, Clark aplica un reservorio lineal con coeficiente de almacenamiento R en la salida para simular la atenuación (almacenamiento en cauces, etc.). En definitiva, los parámetros de Clark son:

• Tc (tiempo de concentración): tiempo que tarda el punto más remoto en drenar al outlet (define la escala del histograma tiempo-área).
• R (coeficiente de almacenamiento): parámetro de atenuación que representa el efecto de retardo y almacenamiento en la cuenca (unidades de tiempo, horas).
• (Opcionalmente, un histograma tiempo-área específico): por defecto, HEC-HMS usa una forma de histograma suave predeterminada (basada en una cuenca elíptica) que solo depende de Tc. Sin embargo, el usuario podría derivar uno de datos GIS para mayor precisión.

Parámetros

En HEC-HMS estándar se ingresan Tc (horas) y R (horas). Con valores por defecto, el programa genera internamente un histograma que asume una distribución de área acumulada At/A = f(t/Tc) con forma curva (se da la fórmula en la referencia: es una función doble potenciada que arranca convexo y luego cóncavo, asegurando una subida suave). Si el usuario dispone de un Time-Area curve detallado (por ejemplo, obtenida dividiendo la cuenca en zonas isocronas via GIS), puede ingresarla; en ese caso Tc serviría para escala temporal y R para atenuación, pero la distribución espacial real se respetará. Generalmente no es obligatorio. El tiempo de concentración Tc se estima como en SCS (suma de tiempos en laderas y cauces) o calibrándolo con hidrogramas observados. El coeficiente R suele calibrarse ya que representa almacenamiento agregado: se puede inferir de la forma del hidrograma observado (un R mayor alarga más la recesión y reduce el pico). Kull & Feldman (1998) sugieren que R físicamente refleja tiempos de retención en la cuenca (por ejemplo, 1/3 del Tc es un punto de partida común). HEC-HMS, por ser lineal, teoréticamente produce colas infinitas del UH; en la práctica, corta el UH cuando el volumen escurrido alcanza 99.5% de la unidad, ajustando el último tramo para conservar volumen unitario.

Clark UH es muy versátil; se adapta a cuencas de cualquier tamaño porque puede incorporar características físicas (tiempos de recorrido) y calibrarse en almacenamiento. Es apropiado tanto en cuencas rurales como urbanas (en urbanas, Tc será menor y R probablemente menor por menores almacenamientos). Con calibración de Tc y R, suele reproducir bien hidrogramas medidos, ya que conceptualmente puede ajustarse tanto en timing como en atenuación. Sin datos, usar estimaciones de Tc y R aún suele ser más realista que asumir formas fijas de UH. Muchos utilizan Clark precisamente por ese balance entre base física y calibración sencilla.

Cabe destacar que HEC-HMS también ofrece una extensión de Clark llamada Clark Variable (Variable Parameter Method) donde Tc y R pueden variar según la intensidad de precipitación excedente (para simular que lluvias más grandes generan respuestas más rápidas y con menos atenuación). Esto añade complejidad y se suele usar solo en investigaciones avanzadas; por defecto se asume Clark lineal constante.

Método Clark Modificado (ModClark)

El método ModClark (Clark Modificado) es un modelo distribuido derivado del Clark UH, que explícitamente considera la variabilidad espacial de tiempos de viaje en la cuenca. En lugar de un histograma teórico, ModClark divide la cuenca en celdas de un grid y asigna a cada celda un tiempo de traslado relativo hasta la salida. Esto permite que la lluvia excedente en cada celda se rotee individualmente a la salida según su distancia/tiempo de viaje, en lugar de asumir el mismo Tc para toda el agua.

Conceptualmente, se calcula un T(t,celda) = T(c,cuenca).Dcelda/Dmax, donde Dcelda es la distancia hidráulica de la celda al outlet o salida del sistema y Dmax la distancia del punto más lejano. Así, a cada celda se le asigna un retraso proporcional. Luego, la escorrentía de cada celda se rutea con un reservorio lineal de parámetro R (se asume el mismo R para toda la cuenca, homogéneo). Finalmente, se suman los hidrogramas de todas las celdas en el outlet. Este método captura explícitamente la distribución espacial de la lluvia: si la lluvia es no uniforme (p.ej. tormenta convectiva sobre una parte de la cuenca), ModClark reflejará la diferencia en tiempos y contribuciones de cada zona, cosa que un UH promedio no haría.

Parámetros

Los requerimientos son: el tiempo de concentración global Tc (horas), el coeficiente de almacenamiento R (horas) como en Clark, y una discretización de la cuenca en grilla con ciertos datos.

La grilla debe contener, para cada celda, su área, y su “distancia de viaje” efectiva al outlet (un índice de distancia hidráulica). HEC-HMS soporta varios sistemas de grilla, incluyendo el HRAP (Polar estereográfica, usado con radar), el SHG (Standard Hydrologic Grid con proyección Albers, tamaños de celda fijos 10m a 10km) y UTM, entre otros.

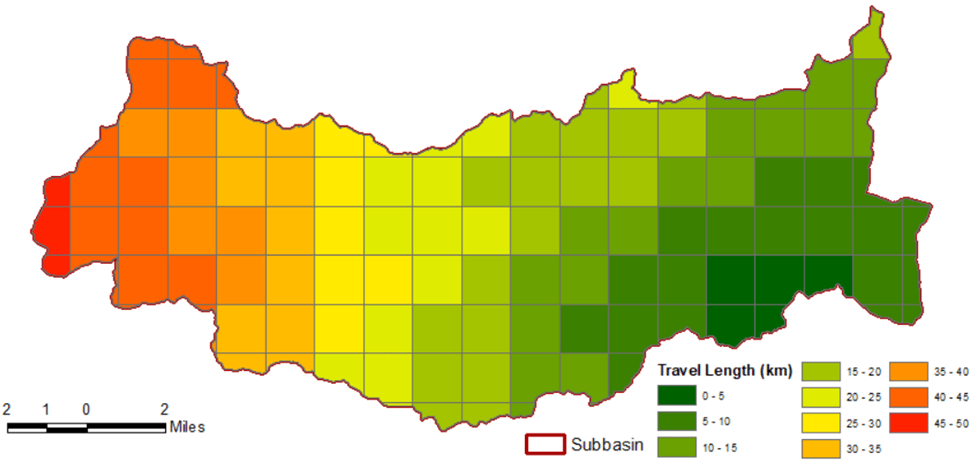
El usuario típicamente obtiene esta grilla a partir de un GIS o de herramientas de HEC-HMS (a partir de la versión 4.4 se introdujeron funcionalidades para generar la discretización). Los datos esenciales por celda son: coordenadas (x,y) del centroide, longitud de flujo Dcelda hasta la salida (en las mismas unidades que Dmax), y área de la celda. En la práctica, un procedimiento es delinear la cuenca en un GIS, obtener un grid DEM, extraer el tiempo de recorrido acumulado (por flujo superficial) para cada celda, normalizarlo y así obtener T(t,celda) relativos. HEC-HMS provee herramientas de importación de estos archivos.

En uso, ModClark también requiere preferentemente un input de lluvia espacialmente distribuido (p.ej. un radar o grilla de precipitación) para aprovechar su potencia; aunque funciona con lluvia uniforme, su beneficio es modelar heterogeneidad espacial.

La complejidad de este método es mayor que Clark tradicional por la preparación GIS necesaria. Es ideal en cuencas medianas a grandes donde la variabilidad espacial de lluvia y tiempo de concentración es importante (por ejemplo, cuencas de cientos o miles de km², tormentas convectivas localizadas). En cuencas muy pequeñas, un UH lumped bastará.

ModClark se puede usar con cualquier método de pérdida (incluso los distribuidos por celda como Green-Ampt en celdas), y con meteorologías como radar NEXRAD.

Precisión esperada: mejora la simulación cuando la lluvia no es uniforme; también puede mejorar la forma del hidrograma al no imponer un solo Tc para todo – esencialmente genera un histograma tiempo-área “real” de la cuenca. Mantiene la suposición de linealidad (usa mismo R para toda la cuenca), lo cual es una limitante (asume mismo efecto de almacenamiento en todos los sub-areas). No obstante, se ha mostrado que con calibración puede imitar resultados de ruteos 2D mucho más complejos con mucha menos carga computacional. Requiere HEC-HMS 4.4+ para crear/leer discretizaciones, y es un puente entre métodos UH y modelos 2D completos.

Método de Onda Cinemática

La onda cinemática es un método de transformación que ya no se basa en UH, sino en resolver simplificadamente las ecuaciones de flujo superficial. HEC-HMS modela la cuenca como uno o dos planos de escurrimiento con flujo hacia un canal colector principal (esencialmente una red en forma de colador: planos que alimentan un canal).

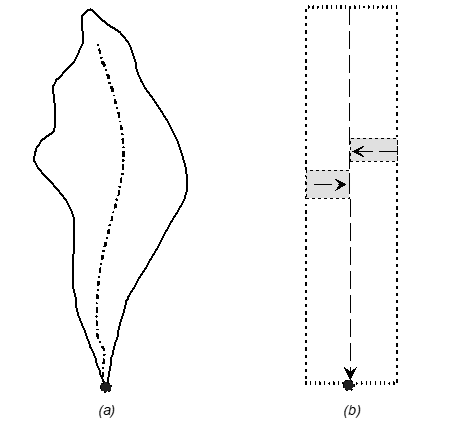
La onda cinemática resuelve la ecuación de continuidad y una forma reducida de la ecuación de momento para flujo superficial: asume pendiente del lecho = pendiente de energía (Sf aproximadamente S0) y desprecia aceleraciones locales y convectivas. Esto permite usar la fórmula de Manning para relacionar flujo y tirante (Q = α A^m con m=5/3 para flujo en lámina sobre plano, o según sección para canal).

La solución consiste en resolver la ecuación diferencial de onda (ecuación de continuidad con esa relación constitutiva) mediante diferencias finitas a lo largo de cada plano y del cauce. En términos simples, la cuenca se esquematiza como varios segmentos en serie: por ej., dos planos (representando ladera izquierda y derecha) fluyendo a un canal central, que a su vez puede subdividirse en tramos para ruteo. El exceso de lluvia actúa como aporte lateral uniforme q sobre los planos (y puede haber aportes definidos a lo largo del canal también). La solución produce hidrogramas de salida en el extremo del canal representando la escorrentía total.

Este método permite representar explícitamente efectos de saturación de los planos: si la lluvia excede la capacidad de infiltración (definida por el método de pérdidas), se genera escorrentía en lámina que avanza con velocidad según la pendiente y rugosidad.

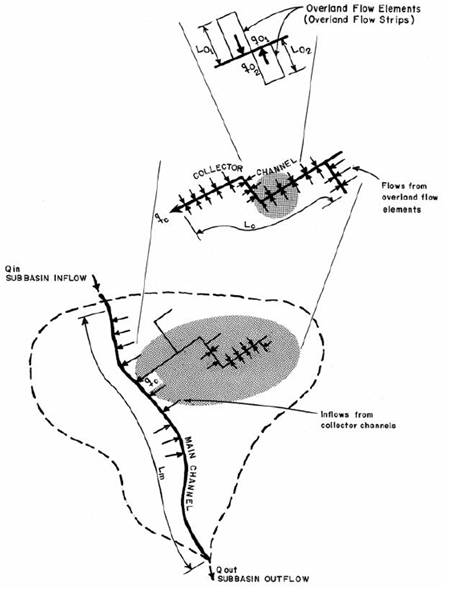
El modelo permite manejar área impermeable separando en dos planos: uno puede asignarse al porcentaje impermeable, con rugosidad distinta, para simular escurrimiento más rápido de calles, mientras el otro plano representa áreas permeables. De este modo se puede captar la respuesta dual en zonas urbanas (HEC-HMS sugiere definir dos planos si se quiere diferenciar escorrentía de área impermeable).

Parámetros

Se deben definir las características geométricas de los planos y del canal: su longitud de recorrido (m), pendiente del terreno (m/m), coeficiente de Manning n (rugosidad) y la porción del área total que drena por cada elemento (ej. Plane 1 = 70% área, Plane 2 = 30% área si se usan dos planos). También se especifica el número de segmentos de ruteo para cada elemento, que es un parámetro numérico para estabilidad (dividir la longitud en X tramos; más tramos = más precisión pero más coste computacional). Para el canal principal, además de longitud, pendiente y n, se debe escoger una sección transversal representativa (HEC-HMS permite rectangular, triangular, trapezoidal o circular idealizada). Cada sección tiene parámetros geométricos (ancho, talud, diámetro en el caso circular, etc.). Importante: la onda cinemática asume flujo a superficie libre (no aplica a tuberías presurizadas; la opción “circular” es solo para simular cunetas con sección redondeada, no tuberías llenas). Los parámetros pueden obtenerse de mapas: la longitud es la distancia de escurrimiento promedio, la pendiente media de ladera, el n de sobreterreno según tipo de superficie (césped ~0.2, pavimento ~0.01, etc.). El canal se deriva del arroyo principal: longitud = talweg, pendiente = pendiente arroyo, sección ~ sección media del arroyo. El número de pasos de ruteo se ajusta para estabilidad (HEC-HMS sugiere empezar con 20).

Aplicabilidad: Este método es apropiado para cuencas pequeñas a medianas donde se desea un modelado más físico del proceso lluvia-escorrentía, por ejemplo en áreas urbanas con superficies impermeables (se puede calibrar n de calles, etc.) o cuencas con pendientes pronunciadas donde la forma de UH fijo puede no responder bien a intensidades variables. También es útil si se necesita conocer hidrogramas intermedios en puntos dentro de la cuenca (ya que se puede obtener salida de cada tramo).

Precisión esperada: Al resolver una dinámica simplificada, puede capturar el efecto de intensidades: por ejemplo, lluvias fuertes generan ondas más rápidas (menor tiempo de concentración efectivo) de forma natural en la ecuación, algo que UH lineales no hacen. No obstante, la onda cinemática no modela retroceso ni efectos de onda dinámica (inundación en valles planos, efectos de represas, etc.), así que en terrenos con backwater puede no mejorar resultados. .

Complejidad: moderada-alta, ya que requiere definir parámetros físicos (aunque en compensación reduce la necesidad de calibrar parámetros abstractos como Tc o R). Con calibración de n y ajustes menores, suele reproducir bien hidrogramas observados en cuencas instrumentadas.

En HEC-HMS, la onda cinemática se configura dentro de la subcuenca; es decir, no hay elementos separados para cada tramo, sino que en la ficha de Transform se indican longitudes, pendientes, n de cada componente (plane 1, plane 2, collector, channel). Debe mencionarse que este método puede ser más intensivo computacionalmente que un UH (pues integra ecuaciones diferenciales), pero manejable para cuencas pequeñas. En el contexto de compatibilidad, la onda cinemática se puede combinar con cualquier método de pérdida. Como nota adicional, solo ciertos métodos de baseflow son válidos con onda 2D (ver más abajo), pero con onda cinemática no se reportan restricciones particulares (ya que la escorrentía base simplemente se sumaría al canal principal como aporte adicional si existiera).

Método de Onda Difusiva 2D

Este es el método de transformación más nuevo en HEC-HMS.

Permite modelar la escorrentía bidimensionalmente sobre la superficie de la subcuenca, resolviendo las ecuaciones de Saint-Venant (onda difusiva) en un mallado 2D. A diferencia de los métodos previos que rutean flujo agregadamente al outlet o salida, el 2D simula el movimiento del agua sobre un terreno representado por una malla de celdas y caras.

Usa un enfoque de volúmenes finitos implícito para la ecuación de continuidad y momento difusiva, permitiendo pasos de tiempo mayores y mayor estabilidad comparado con métodos explícitos. En esencia, se integra un motor de cálculo derivado de HEC-RAS 2D dentro de HMS. Este método no asume linealidad ni uniformidad: modela charcos, ondas que se propagan, flujos subcríticos o supercríticos, etc., de forma más realista.

Es especialmente útil bajo lluvias muy intensas donde la respuesta es altamente no lineal (inundaciones repentinas urbanas, por ejemplo). Se puede combinar con cualquier método de pérdida, canopy y superficie para los procesos verticales, pero restriñe los métodos de baseflow disponibles: únicamente se permiten “Ninguno”, “Reservorio Lineal” o “Baseflow mensual constante” con este transform (métodos como recession, etc., no aplican fácilmente en contexto 2D).

Para usar onda 2D, el usuario debe proporcionar una malla 2D de la subcuenca. Actualmente HEC-HMS no cuenta con un editor gráfico completo de mallas; se debe importar una malla creada en HEC-RAS u otro software, generalmente mediante un archivo HDF de un plan 2D de RAS. La malla 2D contiene: celdas poligonales (triangulares, rectangulares, etc.) con sus relaciones de área-elevación, y caras con sus relaciones de perímetro-elevación-conductancia, precomputadas a partir de un terreno detallado (submodelo de subgrid). Estas relaciones permiten representar la topografía subyacente con celdas relativamente grandes pero incorporando su detalle interno (modelo subgrid). En otras palabras, cada celda 2D tiene un mini-curva volumen-altura, y cada cara tiene su curva área-conductancia-altura calculadas del DEM a resolución fina, dando más precisión sin celdas diminutas. Un punto importante: al importar desde RAS, se pueden incluir condiciones de frontera (ej. conexiones 2D) definidas, excepto la lluvia, que se toma del meteorológico de HMS. Si el usuario no tiene HEC-RAS, puede importar un archivo HDF de malla generado previamente. En el futuro se prevé poder crear/editar mallas dentro de HMS directamente.

Parámetros

Además de la malla misma, se deben ajustar ciertos parámetros numéricos del solver 2D: el factor de peso implícito (generalmente 1.0 para esquema totalmente implícito), las tolerancias de superficie libre y de volumen (criterios de convergencia en altura de lámina y conservación de volumen, típicamente valores pequeños), el número máximo de iteraciones por paso, el método de paso de tiempo (adaptativo vs fijo) y, en caso adaptativo, el Courant máximo y paso máximo (s) permitido; en caso fijo, simplemente el paso en segundos. También se puede habilitar un período de calentamiento (warm-up) para estabilizar condiciones iniciales, con parámetros de duración y fracción de paso. Estos ajustes permiten controlar estabilidad y velocidad: un solver implícito con adaptatividad y múltiple CPU puede simular eventos rápidos con menos pasos y más robustez. Adicionalmente, se puede elegir el número de núcleos de CPU a usar en paralelo, ya que el solver soporta computación multihilo (importante para mallas grandes, usar 4 u 8 cores por ejemplo).

Aplicabilidad: Onda 2D es ideal para situaciones donde la distribución espacial de la escorrentía es fundamental: inundaciones urbanas (drenaje superficial en calles, plazas), análisis de zonas inundables dentro de la cuenca, flujos complejos que no siguen una ruta bien definida por un cauce, o para validar aproximaciones 1D. También para eventos extremos (ej. lluvia muy intensa) donde un UH lineal podría subestimar picos (ya que en la realidad se produce flujo superficial rápido una vez supera capacidad).

Precisión: Este método, al resolver ecuaciones de aguas poco profundas, puede reproducir la dinámica con mayor fidelidad que los UH. Estudios indican que con calibración mínima logra resultados cercanos a modelos 2D completos pero en menos tiempo. No obstante, su costo computacional es elevado comparado con otros métodos en HMS y requiere información detallada del terreno.

Complejidad: muy alta en preparación (construir malla con buen detalle, asignar rugosidades espacialmente, etc.) y en calibración (involucra quizás calibrar rugosidades 2D, pero al menos la mayoría de parámetros son físicos).

Compatibilidad: Como se mencionó, solo ciertos métodos de baseflow pueden emplearse (es lógico, pues baseflow acoplado a un modelo 2D plantearía desafíos; HMS limita a baseflow nulo, lineal o mensual constante). Los métodos de pérdidas funcionan con 2D; de hecho, cada celda puede tener su propia condición inicial y parámetros de pérdida si se configuran como gridded (ej. mapa de CN por celda, etc.). La lluvia puede aplicarse uniformemente o via grilla espacial si se cuenta con precipitación distribuida (recomendable). Un flujo de trabajo típico: diseñar la malla en RAS, calibrar parámetros en HMS con eventos históricos (ajustando Manning n, etc.), luego usarla para eventos de diseño. Este método recién incorporado marca la convergencia de HEC-HMS con modelación hidrodinámica superficial, siendo muy útil para análisis integrados hidrológico-hidráulicos en cuencas.

Hidrograma Unitario Especificado por el Usuario (User-Specified Unit Hydrograph)

Además de los métodos anteriores, HEC-HMS permite al usuario definir directamente un hidrograma unitario personalizado. Esto es útil si se ha derivado un UH a partir de datos de la cuenca o si se quiere emplear un hidrograma sintético de otra fuente. En la práctica, el usuario ingresa una tabla de pares tiempo-caudal que representan el hidrograma unitario (usualmente para 1 mm o 1 pulgada de lluvia excesiva en X horas de duración).

El programa entonces realiza la convolución con la lluvia excedente mediante la suma de respuestas unitarias desplazadas. Si la duración efectiva de lluvia del UH proporcionado difiere de la resolución temporal de la simulación, HEC-HMS aplicará la técnica de S-curve (curva S) para ajustar el UH a la duración adecuada. Básicamente construye la curva acumulada (S) del UH dado, la diferencia a intervalos para la nueva duración y suaviza posibles oscilaciones con un splíne cúbico según se requiera.

Parámetros

Se requiere proporcionar el hidrograma unitario en forma de objeto de datos pareados (tiempo vs caudal unitario) y el número de pases de suavizado (entero) para aplicar al ajuste de la curva S. Adicionalmente, al definir el UH, se debe especificar el intervalo de tiempo de muestreo (ej. 1 hora) y la duración de lluvia excesiva asociada para la cual dicho UH fue derivado. Por ejemplo, si uno derivó un UH de 6 horas de duración de exceso a partir de un evento observado, hay que indicar 6 h. HMS entonces puede generar UH para múltiplos de esa duración por superposición de S-curves. Si se utiliza un UH de duraciones diferentes a las de la simulación, conviene derivar la curva S para escalamiento.

Aplicabilidad: Este método permite máxima flexibilidad – se puede usar en cualquier cuenca si se tiene información suficiente. Sin embargo, en la práctica no es común disponer de un UH fiable: requiere datos de lluvia-escorrentía bien registrados y analizar tormentas unitemporales para deconvolucionar un UH. Además, un UH derivado solo es válido para la duración de lluvia para la que se obtuvo; para otras duraciones hay que recalcularlo o usar la curva S (introduciendo error). Por ello, usualmente se recurre a métodos sintéticos calibrables (como Clark). Este método es útil si, por ejemplo, una agencia ya tiene hidrogramas unitarios típicos para cierta región o si se quiere evaluar un UH proveniente de otro modelo. HEC-HMS también ofrece una variante de “S-Graph especificada”: en lugar de dar el UH, se puede definir directamente la curva S (porcentaje de volumen escurrido vs porcentaje de lag time) y un lag time asociado. Incluso hay opción de un método de regresión para S-graph donde se ingresan parámetros C, L, L{ca}, S, m, p para calcular el lag con fórmula similar a Snyder pero aplicada a curva S. En general, son herramientas especializadas. Si se utiliza UH especificado, la precisión dependerá de la calidad de ese UH. La ventaja es que no hay suposiciones adicionales – es tal cual los datos. Su compatibilidad es completa con pérdidas y meteorología (simplemente convolverá la respuesta).

Consideraciones finales

En resumen, los métodos de transformación en HEC-HMS van desde muy simples (UH predefinido), pasando por paramétricos calibrables (Snyder, SCS, Clark), hasta distribuidos físicos (ModClark, Onda cinemática, Onda 2D). La elección dependerá de la escala de la cuenca, la importancia de la variación espacial, la disponibilidad de datos para calibrar y el fenómeno a estudiar (p.ej. avenidas urbanas rápidas podrían justifican onda 2D; para dimensionamiento de una alcantarilla en zona rural, tal vez baste SCS UH con buen cálculo de Tc).

A continuación y a modo de resumen final, se presenta una tabla comparativa que resume las principales características de estos métodos de transformación, incluyendo los criterios solicitados: datos requeridos, complejidad, aplicabilidad (p.ej. mejor en zonas urbanas o rurales, evento o continuo), precisión esperada y compatibilidad con otros componentes del modelo.

Comparación de los Métodos de Transformación en HEC-HMS

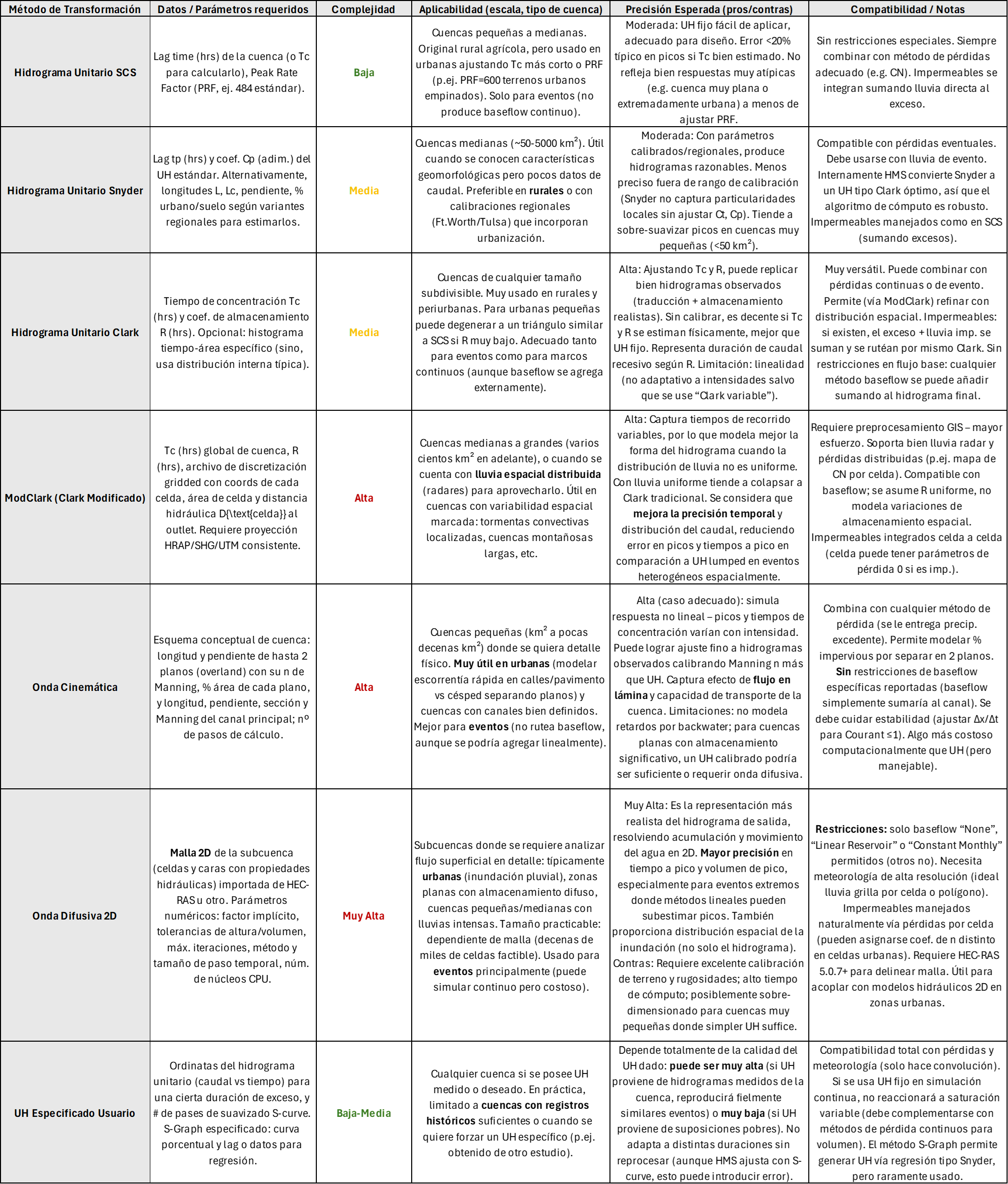
La transformación de la lluvia excedente en escorrentía superficial es un paso clave en cualquier simulación hidrológica. La amplia gama de métodos disponibles en HEC-HMS permite al modelador adaptar el nivel de complejidad del modelo a los datos disponibles y a las necesidades del proyecto. Desde enfoques simples como el hidrograma unitario del SCS, hasta simulaciones hidrodinámicas en 2D, la herramienta ofrece opciones para distintos contextos. En conjunto con un método de pérdida bien seleccionado, estos métodos permiten construir modelos confiables para estudios hidrológicos de diseño, gestión de inundaciones y pronósticos.